Seguimos avanzando después de ver los primeros aspectos de la conducción. Cómo subirse a la moto, cómo frenarla, dónde mirar…, veamos ahora por dónde llevarla. Veamos el camino que tiene que seguir. Veamos La Trazada Ideal.
Hay otras trazadas, y sobre todo hay otra trazada que podemos denominar “en pico”. Tiene dos utilidades: Una para los pilotos que compiten con las motos más potentes, ya sean MotoGPs o ya sean Super Bikes, y dos para el motorista que ha desarrollado ya un control considerable sobre la moto al objeto de ver antes el final de una curva ciega. El primer caso resulta muy interesante desde el punto de vista del aficionado, desde luego, y el segundo resulta de lo más revelador para el motorista en la ruta; pero se trata de un tránsito por el viraje que exige unos recursos mínimos de dominio de la moto, porque tendremos que ser capaces de pararla en un breve espacio y de girarla para encarar el viraje en uno más breve todavía. Así pues, la dejamos en este punto y no la tocamos en este artículo, para que el lector principiante la aprenda en algún curso de conducción o, en cualquier caso con una lección práctica en un escenario adecuado, sin riesgos. Ahora nos centraremos en la base para el que no tiene ni la menor idea de por dónde hacer la curva, para el que anda un tanto perdido e indeciso. Nos centramos en La Trazada Ideal, la línea que sobre el plano y sobre el asfalto hace la curva, sencillamente, más suave, menos pronunciada; en definitiva: más fácil.
Y como en esta serie de artículos tenemos que empezar de algún modo a pasar por una curva, la mejor manera que se me ocurre de comenzar a captar el concepto de esa Trazada Ideal es en la pura teoría y sobre el plano, con dibujos. Me explicaré un poco mejor para que no haya dudas -aunque creo que eso será inevitable. No obstante, invitamos al lector a que pregunte o consulte lo que necesite-:
Esos trazos que se muestran no representan los de una carretera de montaña, ni los de una autovía, ni los del carril dispuesto para el sentido que llevamos. Se trata del asfalto del que se dispone para moverte con un margen de seguridad, sea el que sea, en el escenario en el que se encuentre el lector. Por muy estrecha que sea la carretera y por mucho margen de seguridad que el lector quiera darse por los lados, siempre quedará una franja, aunque sea la comprendida entre las dos huellas de un coche, sobre la que podrá moverse. Bien, se trata de trazar sobre esa franja, tanto si dispone de ese metro y pico marcado por el coche como si son los 12 metros de una pista grande, como puedan ser las homologadas para MotoGP.
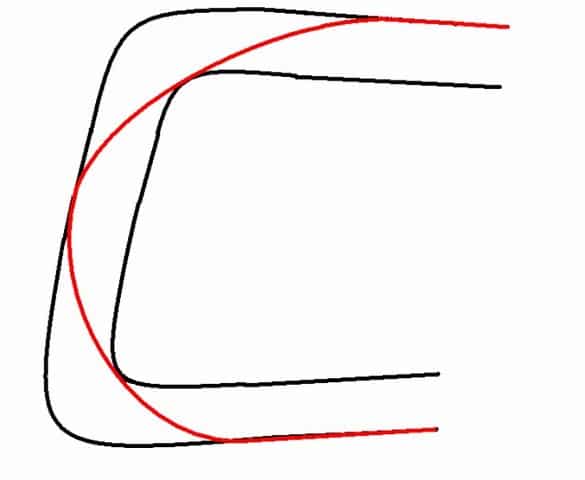
Sobre el plano, la curva más sencilla que nos podemos encontrar es un codo. Presentamos el dibujo de uno con 90º para ver un poco más claro el efecto que produce hacer la trazada ideal.
El principio que marca esta trazada es muy elemental, muy sencillo y siempre, siempre se repite: Del borde exterior, al límite interior y luego otra vez a la línea exterior. Siempre es lo mismo: Exterior, interior, exterior. Lo más importante de este dibujo, en lo que quisiera que os fijarais es en la diferencia entre las dos curvas:
Una: la franja en blanco contenida entre las dos líneas negras.
Dos: la línea roja.
Es fundamental que el lector aprecie la diferencia entre una curva y otra, que vea con claridad cómo la que marca la línea roja es mucho más suave que la franja comprendida entre las dos negras.
Es exactamente el doble de suave. La curva roja es el doble de fácil que la franja en blanco contenida entre las dos líneas negras. Es la diferencia entre seguir la trazada ideal y coger otros caminos, por ejemplo, el que se toma por instinto natural haciendo un calco del trazado original de la curva por la línea media de esa franja en blanco.
Algunos alumnos de los curso de conducción deportiva suelen preguntar:
-¿Cómo es posible que yo vaya con la rodilla metida contra la moto y arrastrándola por el suelo, la estribera de la erre lijándose contra el asfalto y ése otro me pase yendo casi derecho, sin hacer nada, como si se fuera paseando?
El alumno que hace la pregunta, evidentemente, no está siguiendo la trazada ideal, no va por «El Sitio», como se suele decir.
Por otro lado, es importante subrayar también sobre la trazada ideal de ese codo que el momento de empezar a inclinar la moto para buscar el interior lo marca la velocidad que llevemos. Trataré de explicarlo volviendo a la pista con un ejemplo propio, y lo hago allí porque no hay ningún obstáculo ni ningún elemento que intervenga, como en cualquier vía pública, para distraer nuestra atención:
En un circuito, tomas vuelta a vuelta tus referencias para hacer cada curva. Recuerdo un codo semejante a éste (simétrico a la inversa) que no se me daba mal: lo pasaba entero con medio gas. Pero un día vi allí, a pie de pista, una prueba del Campeonato del Mundo de Resistencia y me fijé en las referencias que tomaban aquellos pilotos para inclinarse. Resulta que lo hacían al paso por una garita de control, es decir, empezaban a hacer la curva en plena recta, 50 metros antes de llegar al viraje. El siguiente día que volví a rodar en aquel circuito, utilicé la referencia de los mundialistas: Me tiré a por la curva a la altura de la garita. ¡Qué decirle al lector sobre dónde hubiera ido a parar, si no rectifico a tiempo! Eso es: Exactamente al campo, por lo menos diez metros antes de ni siquiera alcanzar la curva. La velocidad con la que yo alcanzaba ese punto no era, ni muchísimo menos, la de los pilotos del Mundial.
Teniendo en cuenta esto, podremos ver que el quemado de la erre se tirará a por el viraje bastante antes que el harlysta con pasajero y equipaje, a su ritmo de paseo, pero el harlysta también se tirará antes, por poco que sea, de que empiece la curva, si es que quiere seguir la trazada ideal.
Colocamos un par de ejemplos más de trazadas.
Una curva abierta de 180º. Fijaros nuevamente en el ángulo de la curva y en la suavidad de la trazada roja*.
Insisto en que la franja comprendida entre las dos franjas negras no representa la carretera, ni la autovía, ni siquiera el carril del sentido que llevamos: Se trata de la franja de asfalto de la que disponemos, la que nos damos a nosotros mismos, guardando el margen de seguridad que consideremos en ambos lados.
Y éste es especialmente descriptivo. Se trata de lo que se conoce como “una chicane”. En ella vemos cómo se sacrifica la salida de la primera variante (a izquierdas) para hacer bien la entrada en la segunda (a derechas). Para la carretera, la salida siempre tiene una importancia algo más secundaria, mientras que la entrada y sobre todo el paso por el interior son fundamentales. Podemos salir más o menos regular, pero si entramos a contrapié, la curva se nos echará encima, trayendo consigo la inevitable amenaza del desastre.
Para rematar el efecto que hace la trazada ideal sobre una curva, para dar una idea de hasta qué punto puede hacerla suave, fácil, podría haber comprimido un poquito esa misma chicane que he dibujado, o una ese con las dos variantes muy juntas, y veríais cómo la trazada ideal las convierte en una perfecta recta.
¿Hay mejor forma de hacer fácil dos curvas que llegar a transformarlas en una recta?
Y éste es especialmente descriptivo. Se trata de lo que se conoce como “una chicane”. En ella vemos cómo se sacrifica la salida de la primera variante (a izquierdas) para hacer bien la entrada en la segunda (a derechas). Para nosotros, para la carretera, la salida siempre tiene una importancia algo más secundaria, mientras que la entrada y sobre todo el paso por el interior son fundamentales. Podemos salir regular, pero si entramos a contrapié, la curva se nos echará encima y será un desastre seguro.
Para rematar el efecto que hace la trazada ideal sobre una curva, para dar una idea de hasta qué punto puede hacerla suave, fácil, podría haber comprimido un poquito esa misma chicane que he dibujado, o una ese con las dos variantes muy juntas, y veríais cómo la trazada ideal las convierte en una perfecta recta.
¿Hay una forma de hacer más fácil dos curvas que llegar a transformarlas en una recta?
En este vídeo, puede apreciar el lector cómo se muestra (Mejor a partir de 1:40) sobre el propio terreno la trazada ideal:
Ejercicio
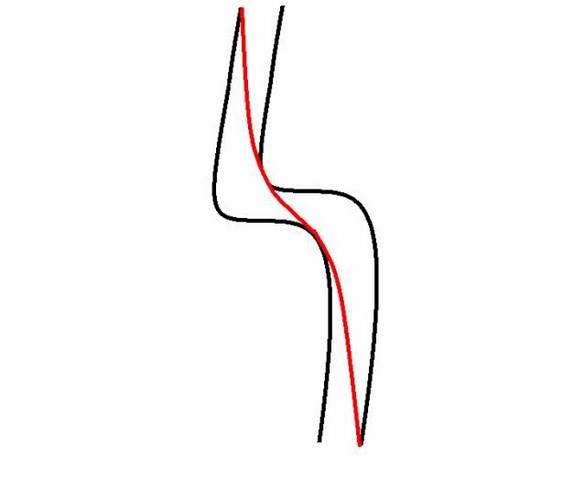
Se trata de que el lector dibuje la trazada ideal de este segmento de asfalto, de hacerlo sólo en el plano teórico, en abstracto; es decir: un escenario en el que no hay árboles, ni coches, ni manchas de gasoil, ni baches, ni badenes, ni tráfico de frente, ni pintura… Se trata de imaginar que sólo se tiene delante ese tramo de asfalto perfecto, liso y uniforme. La cuestión es trazar dentro de las dos líneas negras.
Por supuesto, se recomienda seguir también en este ejercicio el principio fundamental: Exterior, interior y exterior, recordando que cuando se combinan varias curvas, conviene más sacrificar la salida de la anterior para hacer con margen suficiente toda la entrada en la siguiente.
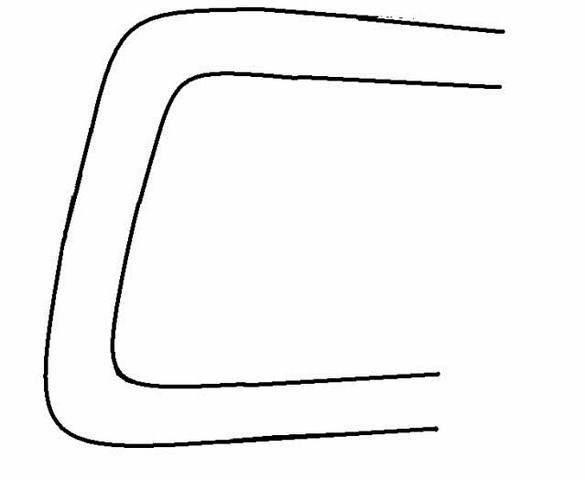
Solución
A la hora de plantear este ejercicio, pensé en las curvas Nieto y Peluqui; pero al final, el dibujo se aparta un poco de esas dos populares curvas de Jerez, porque se alarga la pequeña recta que les separa. En cualquier caso, se trata de un dibujo sobre el plano que lo único que pretende es fijar el concepto.
De todos modos, el punto en el que empieza a buscarse el vértice de la primera curva depende mucho de la velocidad a la que se llegue a ella, como en el caso del codo que se explica en texto princpal del artículo, pero de cualquier forma, también, y aunque se llegue despacio, se adelantará algo a la entrada de la curva. Por otro lado, si vamos muy despacio, cubriremos algunos metros de la recta intermedia con la moto vertical, pero en el momento que se vaya más de prisa, no se deja de ir inclinado. Y ésa es, en definitiva, la esencia del ejercicio: Se trata de ver cómo la trazada ideal hace una sola curva cuando la franja comprendida entre las dos líneas negras dibuja dos.
Para completar los ejemplos, añadimos este dibujo con el recorrido más enrevesado y en donde, teniendo claro el concepto exterior, interior, exterior, no resulta tan difícil encontrar la trazada ideal:









